Gegen jede Intuition.

Wenn es einen mathematischen Satz gibt, den ich als völlig kontra-intuitiv bezeichnen würde, dann ist es der C¹-Einbettungssatz von John Nash.

(Wer den Hollywood-Film “A beautiful mind” gesehen hat: dort wird die ‘Einbettung der Mannigfaltigkeit’ mehrmals am Rande erwähnt.)

Der Einbettungssatz besagt, dass man jede Fläche isometrisch (d.h. abstände-und winkelerhaltend) und C¹ (d.h. einmal stetig differenzierbar) in eine beliebig kleine Umgebung des Nullpunktes im R³ einbetten kann.

Tightly packed curls.

(Einen entsprechenden Satz gibt es dann auch für höher-dimensionale Mannigfaltigkeiten, die man ebenfalls isometrisch und C¹ in einen euklidischen Raum und sogar einen beliebig kleinen Ball einbetten kann.)

Scheinbar absurd

Warum ist dieser Satz scheinbar absurd?

Wenn man eine Fläche in einen Ball vom Radius ε einbettet, sagen wir so dass es auf der Fläche tatsächlich (einen oder mehrere) Punkte gibt, die Abstand ε vom Nullpunkt haben, dann berühren sich in diesen Extrempunkten die Fläche und die Sphäre. Weil die Fläche komplett im Inneren der Sphäre liegt, muß ihre Krümmung mindestens so gross sein wie die der Sphäre (denn die Fläche berührt die Sphäre ja von innen).

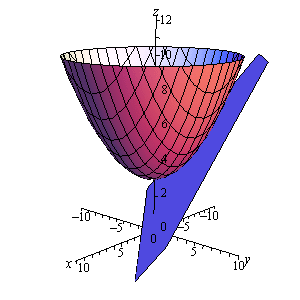
Im Berührungspunkt hat die innere Fläche (rot) grössere Krümmung als die äussere Fläche (blau).

Die Sphäre vom Radius ε hat Krümmung ε^-2.
Die Krümmung der von innen berührenden Fläche muß in diesem Berührpunkt also mindestens ε^-2 sein.

Andererseits sagt aber das Theorema Egregium (Gauß 1828), dass sich die Krümmung einer Fläche bereits aus ihrer Metrik (d.h. aus den Abständen und Winkeln) bestimmen lässt.

Also, wenn man eine gegebene Fläche hat, dann kann man aus ihrer Metrik die Krümmung K in jedem Punkt berechnen – und wenn man die Fläche in einen Ball vom Radius ε (oder kleiner) einbettet, dann ist andererseits aber jedenfalls in einem Punkt die Krümmung mindestens ε^-2, d.h. für das Maximum K_max der Krümmung muß ε≥1/(K_max)^1/2 gelten.

Man kann die Fläche mit ihrer gegebenen Metrik also nicht in einen beliebig kleinen ε-Ball einbetten.

Wo ist der Haken bei diesem Beweis?

Der Beweis benutzt die Krümmung, deren Formel wiederum die zweiten Ableitungen der Einbettung (oder die zweiten Ableitungen der Metrik). Der Beweis funktioniert also nur für 2-mal differenzierbare Einbettungen und beweist dann also, dass man eine Fläche nicht 2-mal differenzierbar in einen Ball vom Radius kleiner als 1/(K_max)^1/2 einbeten kann.

Ohne 2. Ableitung geht’s dann doch.

Wenn man Einbettungen betrachtet, die nur 1-mal differenzierbar sind, dann kann man keine Krümmung mehr definieren (weil in der Formel 2. Ableitungen vorkommen) und der obige Beweis funktioniert nicht mehr. Man würde natürlich erwarten, dass das nur ein technisches Problem ist, dass man den Beweis nur irgendwie modifizieren muß – dem ist aber nicht so.

Völlig unintuitiverweise gibt es solche Einbettungen in beliebig kleine Bälle dann doch, wenn man sich mit 1-mal differenzierbaren Abbildungen zufriedengibt. Das ist die oben im dritten Absatz beschriebene C¹-Version des Nash-Einbettungssatzes, ein völlig anti-intuitiver, technisch aber (im Nachhinein) als nicht besonders schwierig geltender Satz..

Die von Nash später bewiesene C^infty-Version seines Einbettungssatzes besagt, dass man jede Riemannsche Mannigfaltigkeit in einen euklidischen Raum isometrisch C^infty-einbetten kann (natürlich dann, wie oben bewiesen, nicht mehr in einen beliebig kleinen ε-Ball). Diese Version gilt als beweistechnisch sehr viel schwieriger. Zur Geschichte des Beweises und seiner Verbesserungen findet man einiges in der Wikipedia:

The Nash embedding theorems state that every Riemannian manifold can be isometrically embedded into some Euclidean space. Isometric means preserving the length of every path. For instance, bending without stretching or tearing a page of paper gives an isometric embedding of the page into Euclidean space because curves drawn on the page retain the same arclength however the page is bent.

The first theorem is for continuously differentiable (C¹) embeddings and the second for analytic embeddings or embeddings that are smooth of class C^k, 3 ≤ k ≤ ∞. These two theorems are very different from each other; the first one has a very simple proof and is very counterintuitive, while the proof of the second one is very technical but the result is not at all surprising.

The C¹ theorem was published in 1954, the C^k-theorem in 1956. The real analytic theorem was first treated by Nash in 1966; his argument was simplified considerably by Greene & Jacobowitz (1971). (A local version of this result was proved by Élie Cartan and Maurice Janet in the 1920s.) In the real analytic case, the smoothing operators in the Nash inverse function argument can be replaced by Cauchy estimates. Nash’s proof of the C^k– case was later extrapolated into the h-principle and Nash-Moser implicit function theorem. A simplified proof of the second Nash embedding theorem was obtained by Günther (1989) who reduced the set of nonlinear partial differential equations to an elliptic system, to which the contraction mapping theorem could be applied.

The Nash embedding theorem is a global theorem in the sense that the whole manifold is embedded into Rⁿ. A local embedding theorem is much simpler and can be proved using the implicit function theorem of advanced calculus. The proof of the global embedding theorem relies on Nash’s far-reaching generalization of the implicit function theorem, the Nash-Moser theorem and Newton’s method with postconditioning. The basic idea of Nash’s solution of the embedding problem is the use of Newton’s method to prove the existence of a solution to the above system of PDEs. The standard Newton’s method fails to converge when applied to the system; Nash uses smoothing operators defined by convolution to make the Newton iteration converge: this is Newton’s method with postconditioning. The fact that this technique furnishes a solution is in itself an existence theorem and of independent interest. There is also an older method called Kantorovich iteration that uses Newton’s method directly (without the introduction of smoothing operators).

Ein- oder zweimal differenzierbar?

Wir hatten ja letzte Woche schon eine andere Folgerung aus dem Nash-Einbettungssatz, die den Unterschied zwischen 1- und 2-mal differenzierbar verdeutlichte, nämlich den Satz, dass man den flachen Torus isometrisch 1-mal differenzierbar in den R³ einbetten kann, aber nicht 2-mal differenzierbar (aus einem ähnlichen Grund, weil in den ‘Extrempunkten’ die Krümmung positiv wäre).
Ich bin dann per e-Mail gefragt worden, was eigentlich einfache Beispiele von 1-mal, aber nicht 2-mal differenzierbaren Funktionen f:R—>R wären. Ein Beispiel, welches gerne in Analysis I-Übungen gerechnet wird, ist die durch f(x)=x²sin(1/x) für x≠0 und f(0)=0 gegebene Funktion. Hier ist f'(0)=0, aber f'(x)=2xsin(1/x)-cos(1/x) für x≠0, die Ableitung ist also nicht stetig.
Das wahrscheinlich einfachste Beispiel ist aber f(x)=xIxI. In diesem Fall ist die Ableitung f'(x)=2IxI, und diese Ableitung ist zwar stetig, aber kein zweites Mal differenzierbar.

Teil 1, Teil 2, Teil 3, Teil 4, Teil 5, Teil 6, Teil 7 , Teil 8, Teil 9 , Teil 10 ,Teil 11, Teil 12, Teil 13, Teil 14, Teil 15, Teil 16, Teil 17, Teil 18, Teil 19, Teil 20, Teil 21, Teil 22, Teil 23, Teil 24, Teil 25, Teil 26, Teil 27, Teil 28, Teil 29, Teil 30, Teil 31, Teil 32, Teil 33, Teil 34, Teil 35, Teil 36, Teil 37, Teil 38, Teil 39, Teil 40, Teil 41, Teil 42, Teil 43, Teil 44, Teil 45, Teil 46, Teil 47, Teil 48, Teil 49, Teil 50, Teil 51, Teil 52, Teil 53, Teil 54, Teil 55, Teil 56, Teil 57, Teil 58, Teil 59, Teil 60, Teil 61, Teil 62, Teil 63, Teil 64, Teil 65, Teil 66, Teil 67, Teil 68, Teil 69, Teil 70, Teil 71, Teil 72, Teil 73, Teil 74, Teil 75, Teil 76, Teil 77, Teil 78, Teil 79, Teil 80, Teil 81, Teil 82, Teil 83, Teil 84, Teil 85, Teil 86, Teil 87, Teil 88, Teil 89, Teil 90, Teil 91, Teil 92, Teil 93, Teil 94, Teil 95, Teil 96, Teil 97, Teil 98, Teil 99, Teil 100, Teil 101, Teil 102, Teil 103, Teil 104, Teil 105, Teil 106, Teil 107, Teil 108, Teil 109, Teil 110, Teil 111, Teil 112, Teil 113, Teil 114, Teil 115, Teil 116, Teil 117, Teil 118, Teil 119, Teil 120, Teil 121, Teil 122, Teil 123, Teil 124, Teil 125, Teil 126, Teil 127, Teil 128, Teil 129, Teil 130, Teil 131, Teil 132, Teil 133, Teil 134, Teil 135, Teil 136, Teil 137, Teil 138, Teil 139, Teil 140, Teil 141, Teil 142, Teil 143, Teil 144, Teil 145, Teil 146, Teil 147, Teil 148, Teil 149, Teil 150, Teil 151, Teil 152, Teil 153, Teil 154, Teil 155, Teil 156, Teil 157, Teil 158, Teil 159, Teil 160, Teil 161, Teil 162, Teil 163, Teil 164, Teil 165, Teil 166, Teil 167, Teil 168, Teil 169, Teil 170, Teil 171, Teil 172, Teil 173, Teil 174, Teil 175, Teil 176, Teil 177, Teil 178, Teil 179, Teil 180, Teil 181, Teil 182, Teil 183, Teil 184, Teil 185, Teil 186, Teil 187, Teil 188, Teil 189, Teil 190, Teil 191, Teil 192, Teil 193, Teil 194, Teil 195, Teil 196, Teil 197, Teil 198, Teil 199, Teil 200, Teil 201, Teil 202, Teil 203, Teil 204, Teil 205, Teil 206, Teil 207, Teil 208, Teil 209, Teil 210, Teil 211, Teil 212, Teil 213, Teil 214, Teil 215, Teil 216, Teil 217, Teil 218, Teil 219, Teil 220, Teil 221, Teil 222, Teil 223, Teil 224, Teil 225, Teil 226, Teil 227, Teil 228, Teil 229, Teil 230